Prisoner’s Dilemma und was es mit Energie sparen zu tun hat
In der wahrscheinlich ursprünglichen Darstellung, die nach Poundstone (1992, S. 117) von Tucker stammt, ist das Prisoner’s Dilemma eine Geschichte, die von zwei Gefangenen handelt. Sie werden beschuldigt, gemeinsam eine Bank ausgeraubt zu haben. Sie sitzen in getrennten Zellen und die Polizei hat keine Beweise für ihre Tatbeteiligung. Jeder der Gefangenen wird deshalb unabhängig vom anderen vor die Wahl gestellt, das Verbrechen zu gestehen oder zu leugnen. Wenn einer gesteht und der andere leugnet, dann kommt der Geständige frei (Kronzeugenregelung), während der andere die Höchststrafe (15 Jahre) erhält. Wenn beide gestehen, dann erhalten beide eine lange Gefängnisstrafe (10 Jahre). Wenn beide leugnen, also miteinander kooperieren, dann erhalten beide eine kurze Gefängnisstrafe (5 Jahre) wegen unerlaubtem Waffenbesitz. Für jeden der beiden ist Gestehen besser als leugnen, egal was der andere tut, wenn aber beide leugnen, so ist das besser für sie, als wenn beide gestehen. Das Beispiel wird unter anderem bei Luce & Raiffa (1957) beschrieben, die dazu bemerken: „There should be a law against such games!“ (S. 97). Die formale Struktur des Spiels wurde 1950 von Melvin Dresher und Merrill Flood von der RAND Corporation entwickelt, um zu zeigen, dass ein Nicht-Nullsummenspiel genau ein Gleichgewicht haben kann, das allerdings defizitär (nicht Pareto-optimal, siehe unten) ist (Straffin, 1993, S. 73). Das Spiel hat also die Eigenschaft, dass es ein Ergebnis gibt, das beide Spieler besser stellt als das Gleichgewicht.
Prisoner’s Dilemma als experimentelles Spiel
Die Situation läßt sich leicht als experimentelles Spiel modellieren. Die Normalformdarstellung sieht dann so aus wie in der Tabelle. Der erste Beschuldigte hat zwei Optionen, er kann gestehen oder leugnen, und damit die obere oder die untere Zeile der Matrix wählen. Der zweite Beschuldigte hat die gleichen Optionen, er entscheidet damit zwischen der rechten und der linken Spalte der Matrix. In den entstehenden 4 Feldern stehen jeweils die resultierenden Ergebnisse, also die Anzahl der zu erwartenden Jahre hinter Gittern, für den ersten/zweiten Beschuldigten.

Prisoner’s Dilemma – Die Optionen des ersten und zweiten Beschuldigten mit den jeweiligen Ausgängen, die sich aus den Kombinationen ergeben
Überlegungen der am Dilemma Beteiligten
Die Überlegungen des ersten Beschuldigten kann man sich folgendermaßen vorstellen: „Angenommen, ich gestehe den Bankraub, und mein Komplize leugnet, dann komme ich frei, und er erhält 15 Jahre. Angenommen, ich gestehe, und er tut das auch, dann kriegen wir jeweils zehn Jahre. In beiden Fällen bin ich besser dran, als wenn ich leugne, denn dann würde ich fünf bzw. 15 Jahre kriegen. Gestehen verkürzt also meine Gefängnisstrafe um fünf Jahre.“ Dummerweise gelten die gleichen Überlegungen auch für den zweiten Beschuldigten, sodass beide, wenn sie dieser Logik folgen, im Endergebnis auf jeweils zehn Jahre Gefängnis kommen, was nicht das bestmögliche Ergebnis für sie ist. Schließlich hätten sie, wenn sie beide geleugnet hätten, mit jeweils fünf Jahren davonkommen können.
Die spieltheoretische Lösung des Dilemmas
Diese Überlegung kann als umgangssprachliche Formulierung der spieltheoretischen Lösung des Dilemmas angesehen werden. Jeder Spieler hat die Wahl zwischen zwei Optionen, einer, mit der er mit seinem Mitgefangenen kooperiert, und einer, in der er dies nicht tut und nur auf seinen eigenen Vorteil bedacht ist. Die Wahl der nicht kooperativen Option (gestehen) ist in jedem Fall besser für einen Spieler als die Wahl der kooperativen Option (leugnen), wenn die Entscheidung des Anderen nicht bekannt ist. Eine Option oder Strategie mit der Eigenschaft, dass sie unabhängig von der Entscheidung des Anderen immer zu einem besseren Ergebnis für den Entscheider führt, wird als dominant bezeichnet. Eine rationale Analyse der Situation durch beide Gefangene führt also dazu, dass sie am Ende beide ihre dominanten Strategien wählen, was im Beispiel gestehen bedeutet. Dies führt in das spieltheoretische Gleichgewicht, da es für keinen der beiden einen Anreiz gibt, unabhängig vom anderen von seiner Entscheidung abzuweichen. Formal, in der Terminologie von Holler & Illing (2000), ist eine Strategiekombination s* dann ein Gleichgewicht in dominanten Strategien, wenn
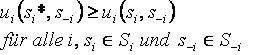
Strategiekombination im Gleichgewicht nach Holler und Illing (2000)
Der Nutzen ui für Spieler i ist also für alle Kombinationen seiner dominanten Strategie si* mit allen Strategien der anderen Spieler s-i größer oder gleich als der Nutzen für Kombinationen von nicht dominanten Strategien des Spielers mit anderen Strategien der anderen Spieler. Wenn dies für alle Spieler i gilt, dann ist s* ein Gleichgewicht in dominanten Strategien.
Da es aber im Beispiel für beide Gefangene besser gewesen wäre, wenn sie beide geleugnet hätten, wird das Gleichgewicht als defizitär oder nicht Pareto-optimal bezeichnet. Ein Ergebnis ist dann nicht Pareto-optimal, wenn es ein anderes Ergebnis des Spiels gibt, das mindestens für einen der beiden Spieler zu einer besseren Auszahlung führt, ohne den anderen schlechter zu stellen. Ein Ergebnis des Spiels ist dann Pareto-optimal, wenn es kein solches anderes Ergebnis gibt, das mindestens einen der beiden Spieler besser stellt. In einem Spiel kann es mehrere Pareto-optimale Ergebnisse geben. Im Prisoner’s Dilemma gibt es genau ein solches Ergebnis, wenn beide leugnen, stehen beide besser da als im Gleichgewicht, in dem beide gestehen. Diese für beide bessere Lösung ist jedoch unter der Annahme der individuellen Rationalität nicht zu erreichen. Das Pareto-Prinzip besagt dagegen, dass ein Ergebnis nur dann als Lösung des Spiels akzeptabel ist, wenn es Pareto-optimal ist. Es ist ein Grundsatz der kollektiven Rationalität. Die beiden Formen der Rationalität stehen also im Prisoner’s Dilemma grundsätzlich im Widerspruch, das ist der Kern des Dilemmas.
Gleichgewicht und Rationalität
Trotzdem wird das Gleichgewicht, das unter der Annahme der individuellen Rationalität resultiert, als Lösung des Spiels bezeichnet. Die Auszahlung im Gleichgewicht heißt der Wert des Spiels. Diese spieltheoretische Lösung der Situation ist zu unterscheiden von dem, was in der psychologischen sozialen Dilemma Forschung unter der Lösung des Dilemmas verstanden wird, nämlich das Erreichen größtmöglicher Kooperation. Dieser Punkt wird auch als Wohlfahrtsoptimum bezeichnet, und er ist immer auch Pareto-optimal. Im Prisoner’s Dilemma entspricht er dem beiderseitigen Leugnen.
Literatur
Holler, M. J., & Illing, G. (2000). Einführung in die Spieltheorie (4. ed.). Berlin: Springer.
Luce, R. D., & Raiffa, H. (1957). Games and Decisions. New York: Wiley & Sons.
Poundstone, W. (1992). Prisoner’s Dilemma: John von Neumann, Game Theory, and the Puzzle of the Bomb. New York: Doubleday.
Straffin, P. D. (1993). Game Theory and Strategy. Washington: The Mathematical Association of America.
